

As already indicated, the intellectual trend has in the past moved away from the idea of actually using formal systems towards using them at one remove. This is responsible for the almost exclusive concentration on first order logic, despite its obvious defects.22 In general we should not be awed by existing foundational systems (as Kant was by Aristotelean logic) but should be prepared to invent our own new ideas. Even quite trivial syntactic changes, like making quantifiers bind more weakly than other connectives (most logic books adopt the opposite convention) can help with the usability of the system!
There are two major foundational schemes for mathematics: set theory and type
theory. These can be traced back to Zermelo and Russell, respectively, and to
their different reactions to the paradoxes of naive set theory. Zermelo felt
that the Russell set {x | x 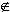 x} was paradoxical because (since so
many sets don't have the property x
x} was paradoxical because (since so
many sets don't have the property x 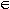 x) it was simply too big
to be a set. Indeed, Cantor had already distinguished between 'consistent' and
'inconsistent' multiplicities, more or less on the basis of size (whether they
were equinumerous with the class of all ordinals). This is called the
'limitation of size' doctrine. Russell, on the other hand, felt that the
problem was with the circular nature of the definition (considering whether a
set is a member of itself), and proposed separating mathematical objects into
layers, so that it only makes sense to ask whether an object at layer n is a
member of an object of layer n + 1, so the Russell set is deprecated as
meaningless on syntactic grounds.
x) it was simply too big
to be a set. Indeed, Cantor had already distinguished between 'consistent' and
'inconsistent' multiplicities, more or less on the basis of size (whether they
were equinumerous with the class of all ordinals). This is called the
'limitation of size' doctrine. Russell, on the other hand, felt that the
problem was with the circular nature of the definition (considering whether a
set is a member of itself), and proposed separating mathematical objects into
layers, so that it only makes sense to ask whether an object at layer n is a
member of an object of layer n + 1, so the Russell set is deprecated as
meaningless on syntactic grounds.
In fact the distinction between set theory and type theory is not clear-cut. Fraenkel added the Axiom of Foundation to Zermelo's set theory, and this gave rise to an intuitive picture of the set-theoretic universe as built up layer by layer in a wellfounded way. (A picture which is nowadays de rigeure among set theorists, and even presented as the motivation for the ZF axioms!) This really amounts to an admixture of type theory, although the layers are cumulative (each layer includes the previous one) and continued transfinitely. What's more, Quine has proposed set theories which, while not having a global notion of type, have a kind of local type discipline based on stratified formulas in the comprehension schema. On the other hand, it seems that Martin-Löf, one of the standard-bearers of type theory, now prefers to refer to his systems as 'Martin-Löf set theory'.
We can still perhaps distinguish types in that they render ill-typed phrases
meaningless, whereas ZF set theory, say, merely makes them false.
Moreover, typing judgements have traditionally been syntactic, or more
precisely, decidable. This is easily true for simple type theory, even with
polymorphism (the Hindley-Milner algorithm generates a most general type for
any well-typed expression). It also holds for systems motivated by the
Curry-Howard correspondence, since after all the corresponding proof
judgements (whether p is a proof of  ) are meant to be decidable. But
though true in principle this often isn't true in practice (many proofs cannot
realistically be normalized), and in some other systems of dependent types,
such as PVS's, typechecking is not decidable even in principle.
) are meant to be decidable. But
though true in principle this often isn't true in practice (many proofs cannot
realistically be normalized), and in some other systems of dependent types,
such as PVS's, typechecking is not decidable even in principle.
Types also arose, perhaps at first largely independently of the foundational schemes originating with Russell, in programming languages. Even FORTRAN distinguished integers and floating point values. One reason was clearly efficiency: the machine can generate more efficient code by knowing more about a variable. For example the implementation of C's pointer arithmetic varies according to the size of the referenced objects. If p is a pointer to objects occupying 4 bytes, then what C programmers write as p + 1 becomes p + 4 inside the (byte-addressed) machine. C's ancestor BCPL was untyped, and was therefore unable to distinguish pointers from integers; to support the same style of pointer arithmetic it was necessary to apply a scaling at every indirection, a significant penalty. Apart from efficiency, as time went by, types also began to be appreciated more and more for their value in organizing programs and providing limited checks on the their correctness. It doesn't seem entirely unreasonable to ascribe some of the same advantages to types in mathematics.
We will concentrate on the practicalities of set theory and type theory as foundations, but it's worth pausing a while to examine the matter philosophically. It seems that there really is a notion of type at work in everyday mathematics; we do think of real numbers as something different from sets of complex numbers, and flattening the whole universe of mathematical discourse into a single undifferentiated realm doesn't seem natural. However the same can be said of any reductive foundationalist programme. In any case, whatever the intuitive appeal of types, ZFC seems to indicate that they are not necessary to ensure consistency.23 There are other special attributes that mathematical objects may have, and 'type' should perhaps just be one of these. Types as primitive can also present awkward choices over whether to formalize some set as a new type or as a subset of (or predicate on) an existing type. In any kind of collaborative programme, it's good policy to avoid giving people too many unnecessary choices (the C programming language and the Macintosh user interface both reflect this philosophy). While on the subject of programming, we might say that sticking to a type discipline is like structured programming, but nevertheless inside the machine, it's all implemented using the equivalent of GOTO statements.
The most direct descendant of Russell's type theory, as simplified by [chwistek], [ramsey-fm] and [church-types], is what is now
called 'simple type theory'. This is successfully implemented in the TPS
prover [andrews-tps] and, with
the addition of a form of polymorphism, in HOL [gordon-holbook]. True to its
name, simple type theory is a simple system, formally and conceptually. In
fact, only a higher-order equational calculus with 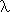 -binding need be taken as basic; as shown by [henkin-ptypes], all the
logical operations can be defined as higher order functions given some
2-element type of propositions.24 The
resulting system is in many ways quite close to informal mathematics; the
types are often helpful and natural, and functions are first-class objects.
However it is rather inflexible in some ways; for example there are no
dependent types (where a type depends on a term, e.g. a type of n
-binding need be taken as basic; as shown by [henkin-ptypes], all the
logical operations can be defined as higher order functions given some
2-element type of propositions.24 The
resulting system is in many ways quite close to informal mathematics; the
types are often helpful and natural, and functions are first-class objects.
However it is rather inflexible in some ways; for example there are no
dependent types (where a type depends on a term, e.g. a type of n 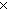 n matrices for variable n). So although
convenient for some parts of mathematics (particularly concrete situations
like number theory and real analysis), it becomes rather inflexible for
other parts, e.g. abstract algebra. However note that some objections often
made to type theory are rather specious. For example, it's true that
R and N are completely different types in simple type theory,
but there are subtyping schemes which can make N
n matrices for variable n). So although
convenient for some parts of mathematics (particularly concrete situations
like number theory and real analysis), it becomes rather inflexible for
other parts, e.g. abstract algebra. However note that some objections often
made to type theory are rather specious. For example, it's true that
R and N are completely different types in simple type theory,
but there are subtyping schemes which can make N  R; in any case this
inclusion also fails in the standard set-theoretic development of the reals.
R; in any case this
inclusion also fails in the standard set-theoretic development of the reals.
There are plenty of more advanced type theories which allow dependent types and other more sophisticated type constructors. Many of these are descended from Martin-Löf's constructive type theories, which are based on the Curry-Howard correspondence between propositions and types, so type constructors correspond to logical operators, e.g. the product type to conjunction. However there is no reason why these systems cannot be used classically. It seems that they are much more flexible than simple type theory, but they are also much more complicated. For example, Nuprl's type theory has over 200 inference rules. Quite how easy it is to formalize mathematics in these systems is still an open question. Many of the researchers are also constructivists, and it is not easy to separate the peculiarities of using constructive logic from the peculiarities of using type theory.
Set theory (e.g. ZFC) is probably the most obvious choice as a foundation. It isn't as simple as simple type theory, and as our earlier remarks indicate, is a rather ad hoc solution to the paradoxes. However it is reasonably simple, and appears to be flexible enough for just about all present-day mathematics. Importantly, it is much better known among mathematicians than type theory.25 There are still question marks over its suitability, even with additional axioms, for some parts of category theory (the category of all sets, etc.) Moreover, some theorems such as recursion on a wellfounded relation need to be stated in an artificial manner using locutions such as proper classes. There are no types to hinder us, but none to help us either. In practice it seems likely that some quite simple abbreviations for set constraints are sufficient to give most of the convenience of types, without irrevocably tying the user to them.
The exact set theory to choose is open to debate. The 'standard' foundation for mathematics is ZFC based on first order logic. However basing the system on higher order logic brings some advantages. Allowing higher order bound variables in axioms like Replacement [gordon-st] extends the power of the set theory26 but makes the axiomatization much neater, without artificial locutions. If the relevant axiom schemas are restricted appropriately, the system is conservative over first order ZFC, but may still offer some advantages such as uniformity of definitional mechanisms [corella-thesis]. There is also the possibility of retaining first order logic, but making classes first-class objects, as in NBG. Some descendants of Quine's set theories admit an embedding of ZF, while providing some convenient additional facilities like a set universe which is a Boolean algebra. Finally, it is possible to add extra axioms, e.g. the Tarski-Grothendieck axiom of universes, or take them away --- for example Replacement is seldom used in mainstream mathematics.27 Mizar settled on Tarski-Grothendieck set theory, after a few experiments with Morse-Kelley. This latter theory, by the way, was the basis for an unusually formal but very elegant book by [morse-sets]; the present author been told that Morse used this formalism in his teaching and research in analysis.
We can judge a foundational system by several criteria: aesthetic and philosophical appeal, flexibility, simplicity and closeness to ordinary mathematical language. These are partly subjective of course. And unfortunately many of them, especially the last two, tend to be in conflict. It seems that at present set theory is the winner, but with more research on different foundational systems, this may change. We do not believe the last word has been said.



 John Harrison
96/2/22; HTML by
John Harrison
96/2/22; HTML by  96/4/5
96/4/5